吴恩达深度学习课程-逻辑回归中的梯度下降和代价函数

在上一篇笔记中，简单记录了逻辑回归和逻辑回归中的梯度下降，这里对上面的梯度下降进行一个详细的解释说明。

梯度下降

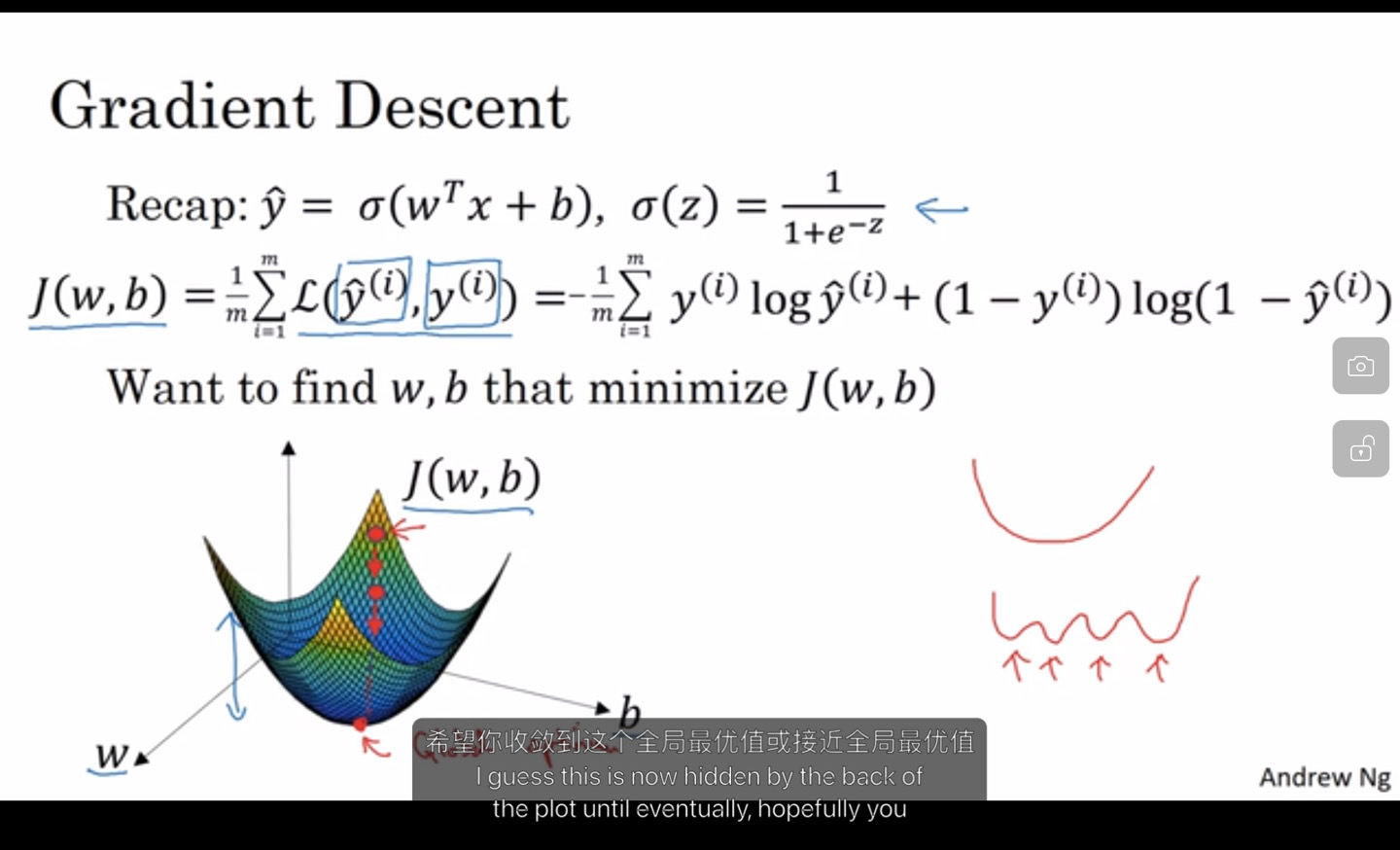] 找到一个合适的w和b的值，使得代价函数 J(w,b)最小。

权值的更新

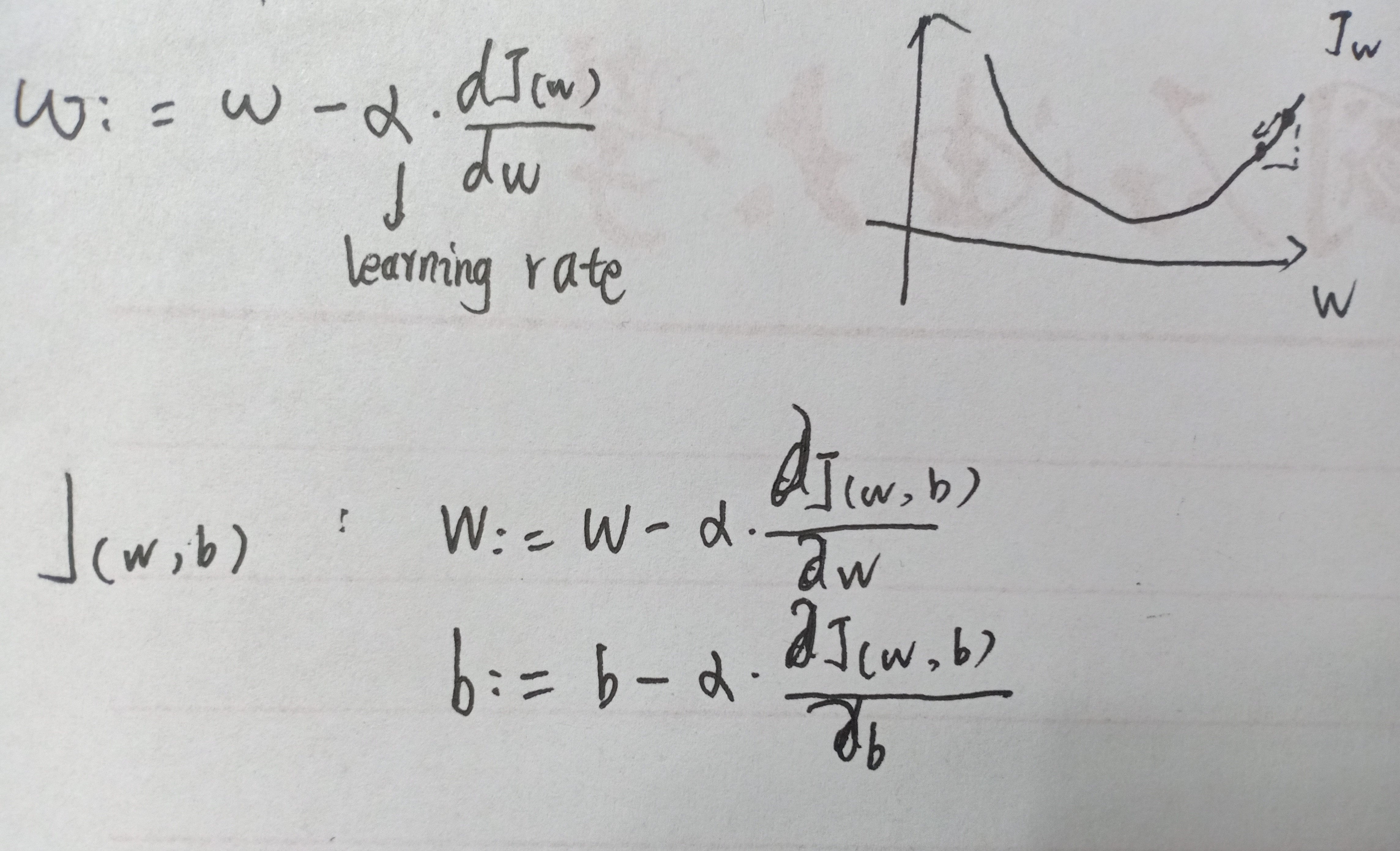
• learning rate 学习率，决定了下降的步伐。w更新后的值。

多样本情况下的权值更新

一般是选择0作为初始值，对样本进行一个参数的迭代更新。这张图里的左半部分是为矢量化的逻辑算法，右边为使用python的numpy进行矢量化计算的处理逻辑。【大量重复数据计算情况下，矢量计算的速度要比循环快的多，无论是在CPU还是GPU上】

逻辑回归中为什么选择上述损失函数

上面直接给了损失函数L和代价函数J，下面记录一下，为什么这么选择

损失函数

代价函数

极大似然估计先来个传送门吧[极大似然估计介绍]( https://www.zhihu.com/question/24124998 "极大似然估计介绍") 【代价函数这个地方，用到了统计学方法中的极大似然估计，关于这个地方，等我再去翻一翻统计学方法这本书再说把。虽然上了这门课，但是着实是没听懂这个数学推导过程】QQQ#### 后记Q今天看了老师的视频，觉得真的是通俗易懂，比单纯看课本要好得多【当然，可能只针对我来说，我可能不适合看书】。但是看了视频，里面一些内容还是比较模糊，比如计算图这个东西，等明天再来吧。向量化，之前觉得不好懂不好写，但是真的了解之后，才会发现向量化的魅力所在啊。 今天还看到一句话，感觉很不错，记录一下：“虽不能至，心向往之”。'